BeeTheory: A New Way to Understand Gravity
What if gravity isn’t a force… but an effect of wave interference?
BeeTheory is an innovative framework that models gravity using wave-based quantum principles.
It doesn’t rely on particles like the graviton, but instead explains gravitational attraction as the result of interference between wave functions. This approach challenges classical and relativistic paradigms, offering a new path toward unifying the fundamental forces of nature.
Why reimagine gravity?
Gravity has long been described — but never truly explained.
- Newton modeled it as a force of attraction between masses.
- Einstein reframed it as the curvature of spacetime caused by mass.
These theories are powerful, but they leave essential questions unanswered:
- Why does gravity exist at all?
- Why can’t we cancel or block it?
- Why is it so weak compared to other forces?
- Why can’t we reconcile it with quantum mechanics?
BeeTheory offers a fresh perspective.
The key insight behind BeeTheory
Every particle can be described by a wave function.
When two particles are near each other, their wave functions overlap slightly.
This interference creates a net directional movement, pulling each particle toward the other — a phenomenon we experience as gravity.
Gravity, in BeeTheory, is not mediated by particles.
It emerges naturally from wave interactions.
This leads to:
- A gravity model with no need for gravitons
- A wave-based explanation compatible with quantum theory
- A framework for modeling gravity across all scales
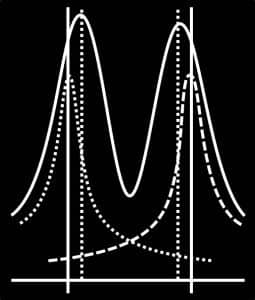
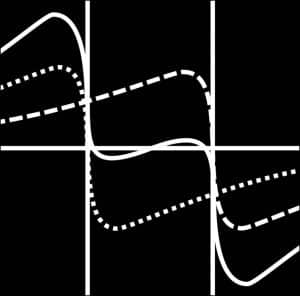
A wave-based gravitational model grounded in physics
BeeTheory is built upon:
- The 3D Schrödinger equation, to describe particles as wave functions in space
- Convolution products, to represent wave interference
- A mathematical structure that replaces the concept of a force field with wave interaction dynamics
This makes it possible to simulate:
- The emergence of gravitational fields
- Particle motion driven by wave convergence
- Wave propagation at both quantum and cosmological scales
What BeeTheory changes
A shift from particles to waves
- No graviton required
- Gravity is an emergent effect, not a fundamental force
A path toward unification
- Electromagnetism, gravity, and quantum fields may all stem from a single wave-based framework
Answers to unresolved mysteries
- Explains phenomena like dark matter as effects of invisible wave structures
- Sheds light on plasma jets, galactic asymmetries, and wave-based gravitational pulses
- Offers insight into why gravity behaves the way it does
A universe woven by waves
Beyond equations, BeeTheory proposes a different view of reality.
Instead of separate particles and fields, we see a continuous fabric of wave interactions.
This implies:
- Seamless connection across all scales — from subatomic to galactic
- A reinterpretation of matter, energy, and consciousness as wave-based expressions
- A philosophical shift toward unity and interconnectedness
The wave does not carry reality.
The wave is reality.
Explore BeeTheory in depth
Foundations
- Mathematical model of BeeTheory
- Why gravity might not be a force
- Wave-based quantum mechanics: Schrödinger revisited
Implications
- Hidden mass and wave structures
- Waves, consciousness, and ethics
- The bridge between science and spirituality
CTA buttons to include:
→ Read the full articles
→ See 3D simulations
→ Download the summary PDF